Meta-analisi: definizione e modelli

È possibile aggregare i risultati di diversi studi su uno specifico argomento e trarne conclusioni statisticamente valide? La risposta è sì! La meta-analisi è uno degli strumenti statistici più avvincenti per raggiungere proprio questo obiettivo. Utilizzando tutto ciò che un campo del sapere è stato in grado di produrre, essa ha il compito di trarre informazioni numericamente valide dalla combinazione di diversi studi sullo stesso argomento. Ma come paragonare apples to apples, quando queste appartengono varietà differenti, come gli studi eseguiti su differenti campioni)?

Definizione di meta-analisi

Formalmente la meta-analisi è definita come quella tecnica statistica idonea a combinare i risultati di diversi, ma similari studi, permettendo non solo una loro comparazione, ma, quando possibile, anche l’individuazione di un’univoca conclusione su un determinato argomento. Il termine “meta-analisi” si riferisce infatti a quel tipo di analisi dei dati che si ottiene collezionando i risultati di studi che hanno risposto a similari domande di ricerca su uno specifico argomento.

Questo significa che la meta-analisi ha come base fondamentale la comparazione tra studi che non solo hanno in comune l’argomento principale, ma hanno una similare domanda di ricerca principale a cui rispondere. Questo fa sì che non tutti gli studi su uno stesso argomento siano comparabili. In meta-analisi è possibile valutare solo quegli studi che hanno risposto ad una stessa domanda di ricerca, seguendo una similare procedura. In altri termini, non è possibile comparare “apples and oranges“!

Un esempio: quantità di sonno ed insorgenza cancro

Ad esempio, potremmo chiederci se la quantità di sonno agisce con elemento determinante (o fattore di rischio) nell’insorgenza cancro. Abbiamo tre possibili soluzioni, più o meno complesse e affette ognuna da qualche tipo di bias.

Il primo e più diffuso approccio è quello di condurre uno studio su un campione di pazienti già ammalati e comprendere il loro approccio al sonno prima dell’insorgenza della malattia. Il secondo approccio consiste nel valutare l’insorgenza cancro nel corso di un certo periodo di tempo in una determinata popolazione, monitorando appunto la quantità (e forse anche la qualità) di sonno della popolazione osservata. Sebbene entrambi i metodi siano efficaci nel produrre una risposta alla domanda di ricerca, essi non sono comunque esaustivi.

Il terzo approccio è quello di effettuare una meta-analisi. Utilizzando i risultati di similari studi condotti nel tempo da vari ricercatori, è possibile fornire una conclusione, generalmente valida, sul tema della correlazione tra quantità di sonno e insorgenza cancro. Essa inoltre può essere il trampolino di lancio di un trial, in quanto ci permette di effettuare di identificare in modo corretto le domande di ricerca e gli obiettivi primari e secondari del nostro futuro trial.

Meta-analisi: output e modelli.

Cosa misura la meta-analisi?

Ogni meta-analisi fornisce come risultato i cosidetti effect sizes (definiti anche treatment effects in statistica medica). L’effect size descrive l’intensità di un trattamento o, più genericamente, la forza della relazione tra due variabili.

Se gli studi primari hanno come risultato un outcome binario (successi/fallimenti di una terapia), gli effect sizes della meta-analisi saranno calcolati in termini di  odds ratios e di risk ratios. Se i risultati degli studi primari sono rappresentati da outcome continui (medie e deviazioni standard), allora il risultato della meta-analisi sarà rappresentato da misure come la g di Hedges e la d di Cohen. La meta-analisi determina l’effect size di ogni studio, assegna la consistenza dell’effetto tra gli studi ed, infine, calcola l’effetto complessivo.

Modelli

Come si può notare da quanto detto sinora, esiste una prima grande distinzione di meta-analisi rispetto al tipo di dato (classico problema statistico iniziale). Il secondo problema è la valutazione della differenza tra studi (cosiddetta eterogeneità). Gli studi non sono tutti uguali, alcuni differiscono nel metodologia, altri per il campione utilizzato, altri per gli strumenti statistici utilizzati e così via.

Al fine di condurre una buona e valida meta-analisi è necessario tenere conto di questi elementi. L’eterogeneità è quindi una dei grandi protagonisti di una meta-analisi. Ha il compito di misurare le variazioni tra i differenti studi, comprendendo se la variazione (elemento fondante della stessa statistica) è una semplice fluttuazione del campione (pertanto ineliminabile), oppure è il risultato di una reale variazione tra gli studi dovuta a differenze metodologiche e nel caso medico, cliniche.

A seconda del livello di eterogeneità, definito e motivato dal ricercatore, la meta-analisi si esegue seguendo uno dei seguenti modelli: common-effect, fixed-effects e random-effects.

Il primo modello – common-effect – definito anche fixed-effect (attenzione alla mancanza di una “s”, particolare che lo distingue dal più famoso modello fixed–effects), si applica quando si può assumere che gli studi sono uno la replica esatta dell’altro (per dire in modo molto semplice).

Il modello fixed-effects (attenzione alla presenza della “s”) assume che gli studi hanno effect sizes differenti e che questi ultimi siano sempre fissi. In altre parole, gli studi primari, considerati tutti insieme, rappresentano la popolazione di interesse e la variazione è quantificabile, oltre che fissa.

Il terzo modello (random-effects) è quello maggiormente applicato. Esso assume che gli studi sono tra loro eterogenei e che rappresentino un campione random.

Scegliere il modello corretto è necessario per effettuare una buona meta-analisi. La scelta non è una mera osservazione di un numero. Essa è sempre frutto di una valutazione accurata e logica, di cui il valore numerico rappresenta l’ultimo aspetto.

Come presentare una meta-analisi?

Il miglior metodo per sintetizzare i dati di una meta-analisi è quello di costruire un forest plot. Si tratta di un grafico sul quale sono riportati gli effect sizes (con i relativi CI) dei singoli studi e il loro effect size globale (con il relativo CI). L’aspetto di un forest plot è quello presentato nella seguente immagine.

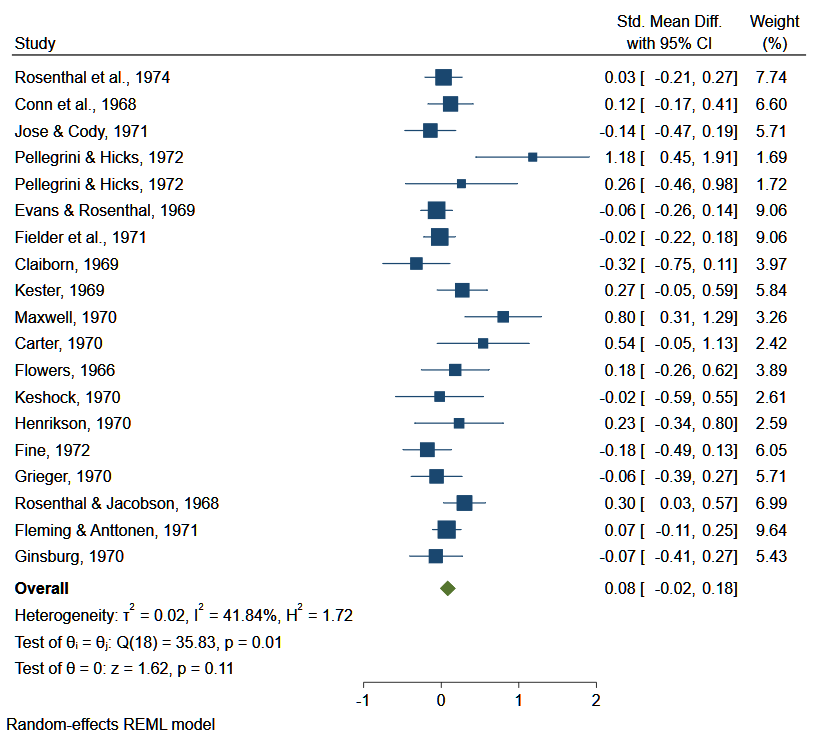
Dal forest plot è estrarre molte informazioni: l’effect size di ogni studio, l’effect size complessivo (dati presenti nella colonna “Std. Mean Diff.”), il peso di ogni studio (colonna “Weight”, oltre che quadratini colorati), l’eterogeneità, la percentuale di eterogeneità (I²) ed alcuni test statistici sul valore di theta (il vero e sconosciuto effect size).

Conclusione

La meta-analisi è uno strumento potentissimo ed utilissimo in molti campi scientifici e specialmente in quello medico. Eseguire tecnicamente una meta-analisi non è un mero esercizio statistico. Essa è il frutto di un più ampio lavoro di conoscenza e logica nell’aggregare gli studi e nel trattare i risultati presenti in essi. La meta-analisi è complessa ed interessante. È possibile eseguirla come studio introduttivo prima di un trial oppure come ambito di approfondimento su un argomento. Lo scopo è duplice: può far emergere una conclusione univoca su un argomento ed aprire la scienza a nuove e più specifiche domande di ricerca.