Indice Show
Lavorando con misurazioni provenienti da diversi strumenti di misura o da diversi esaminatori ci si imbatte spesso nel problema del calcolo dell’agreement, versione inglese dell’italiano “accordo” o “concordanza”. In statistica, il più noto strumento per la misurazione dell’agreement in statistica è il plot di Bland-Altman. Come interpretare in modo appropriato questo potente plot? Scoprilo continuando a leggere.
Agreement: cosa significa?
L’agreement in termini statistici serve per indicare il livello di accordo tra due diversi metodi di misurazione o tra due osservatori che misurano lo stesso fenomeno. Molto spesso nel linguaggio dei non addetti ai lavori, l’agreement è confuso con la correlazione. Tuttavia, i due concetti statistici partono da presupposti diversi, hanno finalità diverse e usano formulazioni diverse.
Mentre la correlazione ha lo scopo di misurare quanto al variare di x si osserva una variazione di y e viceversa (per ulteriori indicazioni, leggi il mio articolo dedicato), l’agreement vuole determinare il grado di accordo tra x e y, siano esse due misurazioni con diversi strumenti o eseguite da due osservatori. Questo significa che non solo le misurazioni devono variare nella stessa direzione, ma devono essere tra loro prossime.
L’agreement prende anche le distanze dalla regressione o dall’uguaglianza delle medie, in quanto la semplice risposta positiva ad una regressione o ad un’analisi di uguaglianza di due medie (ed attenzione ad interpretare il p-value non significativo), non significa certo che le due misurazioni sono d’accordo. Gli errori tra le due potrebbero essere così ampi da rendere tutto completamente distorto. O ricco di bias se ti piace di più!
Plot di Bland-Altman
Il metodo più noto per la misurazione dell’agreement in caso di variabili quantitative è il plot di Bland-Altman. Il fondamento teorico del plot è molto semplice: più la differenza tra due variabili x e y per ogni osservazione è prossima a zero, più le due misurazioni sono in accordo.
Questo comporta che il punto di partenza del plot di Bland-Altman è la differenza, osservazione per osservazione tra y ed x, ossia:
d = y – x
Se le differenze sono distribuite in modo randomizzato intorno al valore zero e nessuna delle differenze è molto ampia, allora si dice che l’agreement è buono, cioè le misurazioni sono tra loro in accordo.
Il plot di Bland-Altman è un grafico che partendo dalle differenze appena descritte combina, o meglio tecnicamente “plotta”, il valore delle differenze rispetto alla media della semi-somma delle due variabili, ossia:
`\text{media}(\frac{x+y}{2} )`Il risultato di questo plottare è il grafico-esempio riportato nella seguente Figura 1.
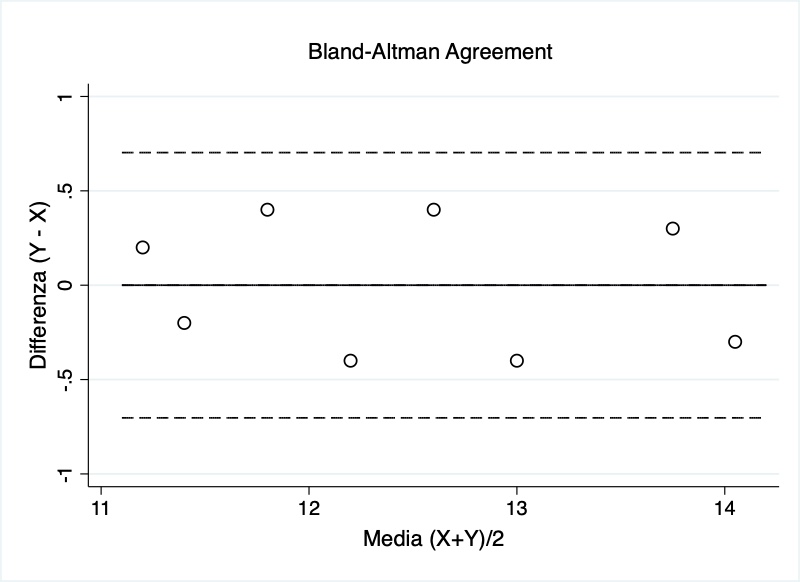
Interpretare il plot di Bland-Altman
La lettura del plot è semplicissima. Segue il comune buon senso: due misure sono tra loro in accordo se le loro differenze rientrano in un range di tollerabilità del 95%. Le due linee orizzontali tratteggiate in Figura 1 sono proprio i limiti dell’agreement, o come preferiscono alcuni autori, i limiti del disagreement, ossia del disaccordo.
In statistica quando misuriamo il livello di concordanza di due misurazioni rispetto ad una stessa variabile, la differenza d non è altro che l’errore di misurazione. Affinché il plot di Bland-Altman sia efficace, è necessario che questo errore si distribuisca secondo la famosissima curva Gaussiana.
Ne deriva che i limiti dell’agreement sono definiti in base alla seguente formula:
d ± 1.96 sd
di cui il valore sd altri non è che la deviazione standard delle differenze.
Limiti dell’agreement tra statistica e clinica
Come hai appena visto il plot di Bland-Altman e la statistica ci consentono di determinare se due misurazioni o una misurazione eseguita da due osservatori sono tra loro in accordo. Il calcolo dei limiti dell’agreement è una componente fondamentale per dire se e quanto le misurazioni concordano. Tuttavia, avere dei buoni limiti che siano in accordo con la sola statistica, può divenire pericoloso per l’interpretazione dei risultati in ambito clinico. Il lavoro di un buon statistico non è solo elaborare numeri, ma è riportare quei numeri nel loro contesto originario.
Nel caso del plot di Bland-Altman e più in generale di tutte le misure di agreement ciò che fa la differenza tra un buon lavoro ed un pacchetto di numeri senza altro scopo che sprecare un pò di carta, è dato dalla valutazione se le misurazioni rientrano nei limiti clinici della misurazione osservata.
Mi spiego meglio. Consideriamo il caso del calcolo dell’emoglobina (Hb) da parte di due diversi tecniche di misurazione. Se i limiti di agreement fossero ad esempio pari a -0.4 g/dL e +0.4 g/dL, per quanto i valori siano numericamente e statisticamente perfetti, non sarebbero però validi per le attuali tecnologie che hanno un livello di precisione e di accuratezza molto molto elevato.
Se prendessimo per buona una tale misurazione, significherebbe che le due tecniche di misurazione dell’emoglobina sono sempre in accordo, quando invece per i valori clinici consentiti dalle attuali strumenti ciò potrebbe non essere vero!
Conclusione
Riassumendo, misurare l’agreement tra due misurazioni o su una misurazione eseguita da due osservatori è un processo statistico molto semplice. I software sono in grado di supportare e facilitare i calcoli, ma attenzione ciò non significa che si ha sempre ragione quando si riporta il problema nel contesto clinico. Non finirò mai di ripeterlo: i numeri sono solo numeri, spetta a chi li elabora e chi li utilizza dare ad essi il senso della realtà osservata.











