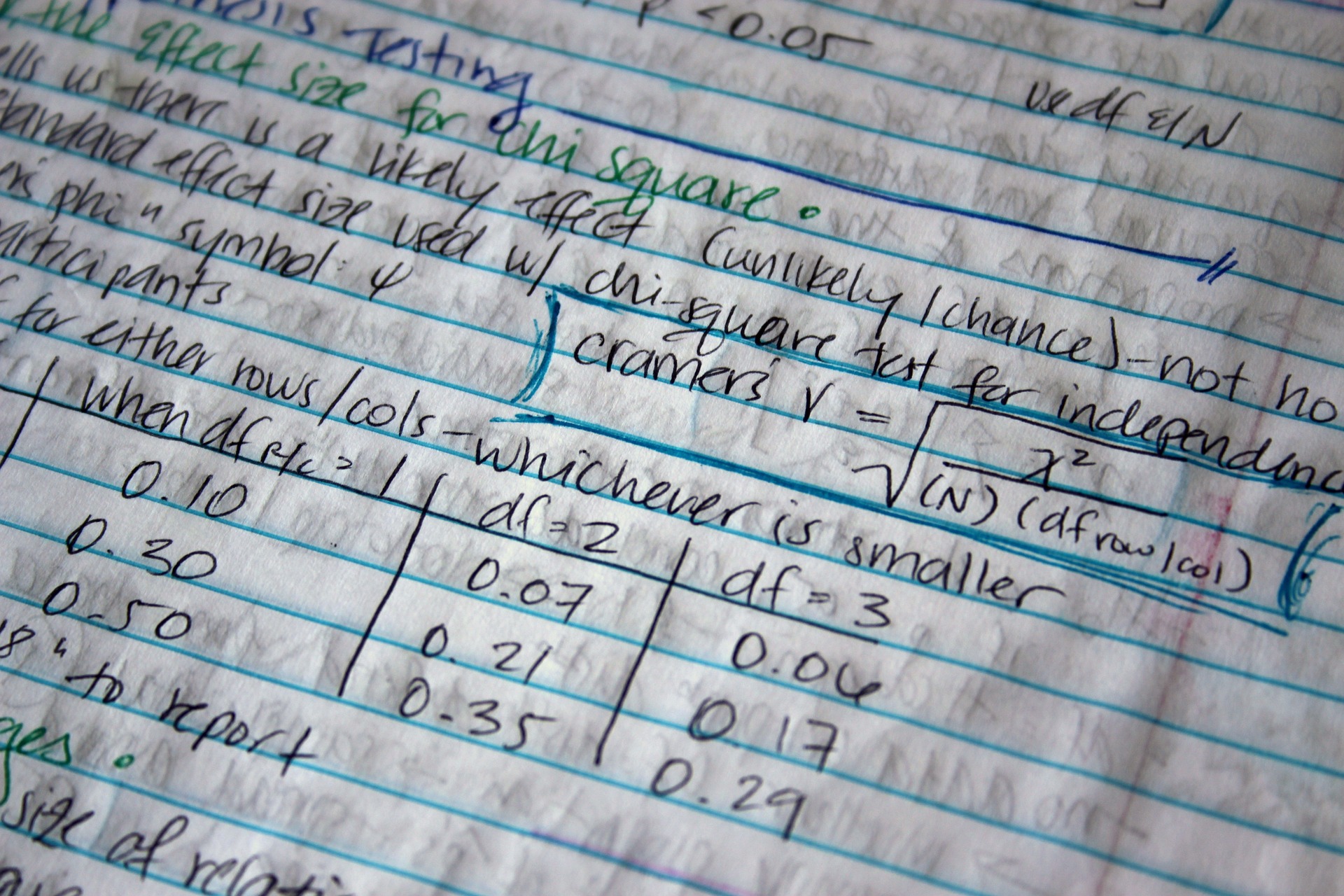Indice Show
Il p-value è sotto 0.05, sei sicuro che la tua ipotesi sia correttamente dimostrata? Secondo molti, un p-value significativo è la chiave di volta per spiegare ogni fenomeno. Siamo proprio sicuri che sia sempre così? Per rispondere alla domanda circa la corretta dimostrazione dell’ipotesi di ricerca e quindi derivare dalla sua risposta la positiva risoluzione dello studio sperimentale, bisogna innanzitutto capire cosa indicano il p-value e la sua “famigerata” soglia del 5%.
Il valore di p è utilizzato quale strumento di lettura dei test statistici. Protagonista di tutti gli studi che siano di statistica medica o di econometria, il p-value compare in ogni angolo. Ma, a differenza del pensare classico circa la valenza, oserei dire la supremazia del p-value, la statistica come scienza che studia i dati fonda sul p-value e sul concetto di significatività solo una parte della sua certezza. Un valore di p minore di 0.05 non significa che la tua ipotesi è vera. Così come un valore di p maggiore di 0.05 non comporta che la tua ipotesi sia errata.
Il p-value: il grande risolutore per i test statistici
Gli studenti di statistica sono pratici con molti degli strumenti e dei test statistici più diffusi: chi quadro, t-test, U Mann-Whitney sono solo alcuni dei nomi più popolari di test statistici in statistica inferenziale. Tutti questi strumenti sono accomunati da un indicatore: il p-value e la conseguente significatività. Il valore di p rappresenta il dramma di moltissimi studenti: come si legge questo p-value? Come deve essere il suo valore: inferiore o superiore alla soglia fissata?
La risposta a quest’ultima domanda è: dipende! La statistica così come tutta la scienza, non fonda la sua forza su preconcetti, ma su ipotesi. Per sapere cosa comporta un p-value maggiore di 0.05 o minore di 0.05, la risposta dipende da cosa stai cercando e da cosa vuoi dimostrare! Nella maggior parte dei test il p-value minore di 0.05 è fondamentale; altre volte non è male un p-value maggiore. Dipende tutto dall’ipotesi del test statistico che stai adoperando!
Il termine p-value sta ad indicare il valore di probabilità. Più concretamente esso indica la probabilità che quanto stiamo sostenendo sia corretto con un piccolo margine di errore. Oppure esso spiega che la probabilità di sbagliarsi è troppo alta per sostenere la veridicità di quello che ipotizziamo.
P-value minore di 0.05
Supponi di voler dimostrare che il peso dei pazienti sottoposti ad uno specifico regime dietetico migliora dopo un certo periodo. Per fare ciò, potresti creare un gruppo di controllo, ossia un gruppo di pazienti con caratteristiche alle baseline simile in tutto e per tutto a quello di trattamento, ma non sottoposto a quella specifica dieta. Lo scopo di un tale study design sarebbe dimostrare che la dieta migliora il peso dei pazienti, ipotizzando che il peso del gruppo di trattamento alla fine del periodo di dieta è inferiore a quello del gruppo di controllo.
Poiché in generale il peso tende, almeno sui campioni con una buona numerosità campionaria, a distribuirsi normalmente, possiamo utilizzare il test t per valutare la differenza in media tra i due gruppi. La classica lettura del test t prevede che se il p-value è superiore alla soglia fissata (classica la soglia del 5%, ossia 0.05), allora significa che non vi è differenza statistica sulla variabile peso tra i due gruppi, mentre se, al contrario, il p-value è inferiore a 0.05 (p < 0.05), allora c’è differenza statisticamente significativa tra i due gruppi. Leggendo i valori in media, possiamo anche dedurre che se il peso del primo gruppo è inferiore a quello del secondo, allora è possibile affermare che effettivamente, salvo fattori confondenti o cause di bias, lo specifico regime dietetico sperimentato riduce il peso. Insomma c’è significatività.
P-value < 0.05: problema risolto ed ipotesi di ricerca dimostrata?
Per molti studenti e ricercatori, dimostrare la significatività del test statistico è di per sé sufficiente per affermare che lo studio è stato dimostrato. Tuttavia, specialmente nel caso delle pubblicazioni scientifiche, tale certezza si può trovare molto presto a fare i conti con le domande dei revisori. Questi ultimi, esperti nel loro specifico ambito e particolarmente allenati a riconoscere le pecche degli studi scientifici, possono chiedere di dimostrare, numeri alla mano, che la significatività sostenuta nei risultati non sia una sovrastimata.
Nei ricercatori alle prime armi, il primo impatto con tale genere di richiesta è la rabbia, il secondo il rifiuto, il terzo è lo sconforto. La domanda del revisore è l’inizio di un baratro statistico. Ma, se guardiamo attentamente e con un pò di calma, la domanda non preclude l’accettazione dell’articolo. Essa è infatti finalizzata a spingere l’autore a rinforzare le sue ipotesi. La domanda infatti è il punto di avvio per dimostrare potenza del campione ed effect size, ossia è quel passaggio necessario per far capire che la significatività dimostrata non è fondata nella sabbia, ma nella più forte e solida roccia della comprensione di cosa si stia statisticamente sostenendo.
I concetti di potenza ed effect size sono il corredo necessario della significatività in quanto consentono di capire se le differenze statistiche segnalate dal test siano il frutto di una certezza o di una sovrastima dell’effetto, ossia di un qualcosa che apparentemente sembra esserci, ma di fatto si tramuta in un nulla di fatto alla prima seria prova di validità. In altre parole, il p-value ci consente di capire se vi sono differenze statistiche, ma non dà la certezza assoluta di aver ragione.
Cosa succede se il p-value è maggiore di 0.05?
Dunque il p-value minore di 0.05 non è fonte di certezza, ma cosa dire di un p-value maggiore di 0.05? Ritorniamo qui al discorso del dipende. Ci sono alcuni casi in cui un p-value superiore alla soglia di 0.05 non solo è positivo, ma per semplificare il lavoro statistico successivo è auspicabile. Un esempio classico è il p-value del test di normalità Shapiro-Wilk.
L’ipotesi nulla del test di Shapiro-Wilk afferma che la variabile osservata è distribuita normalmente, ossia se ciò è vero possiamo applicare tutti i più belli test statistici, dal test t di Student fino alla correlazione di Pearson, per non parlare dell’uso di tali variabili in modelli di regressione. Ma se questa è l’ipotesi nulla, come vorremmo il p-value? Ovviamente maggiore di 0.05, ossia un p-value che ci consenta di affermare che non vi è alcuna evidenza che la variabile sia distribuita in modo non-normale. Un p-value minore di 0.05 ci costringerebbe a rifiutare l’ipotesi nulla e dunque perdere quel bellissimo apporto che le variabili distribuite normalmente forniscono ai ricercatori, specialmente quelli più inesperti.
Attenzione alle ipotesi
Prima di concludere voglio farti notare un particolare: nel sostenere l’ipotesi nulla, non ho affermato che la variabile si distribuisce normalmente, ma ho scritto che non ho prova che non si distribuisca normalmente. In altri termini, il p-value superiore allo 0.05 non fornisce un nuovo scenario, ma consente solo di affermare ciò che non posso sostenere perché non ci sono prove.
Tale concetto vale sia per il test di normalità sia per il precedente test t. Tornando all’esempio precedente del confronto del peso di due gruppi di pazienti (trattamento vs. controllo), nel caso l’esito dell’analisi di significatività del test t fosse un p > 0.05, non possiamo affermare che i due gruppi sono uguali, ma possiamo unicamente affermare che non vi è evidenza statistica (significatività) che essi siano diversi. Questo è un passaggio statistico fondamentale. Alcuni studi con un p-value non significativo concludono che due fenomeni comparati sono uguali. Tale interpretazione, per svariate ragioni, inclusa la dimensione del campione, non può scaturire unicamente dal valore di p-value. Essa deve essere il risultato di un percorso logico che tiene conto di altri elementi statistici.