Indice Show
Alcuni strumenti statistici risultano, per chi ci lavora ogni giorno, più affascinanti di altri. La curva di sopravvivenza Kaplan-Meier è, per me, uno di questi. Mi piace tracciare, anche con semplici programmi di calcolo, gli “scalini” di questa curva. Alcuni ricercatori con cui lavoro, parlando della Kaplan-Meier la definiscono la “curva della speranza”. In effetti, il suo grandissimo uso in ambito medico specialmente per le patologie più gravi, consente di dare speranza a molti pazienti che hanno appena ricevuto una pesante diagnosi. Essa riceve inoltre un notevole applicazione nell’ambito epidemiologico lavorando in modo più performante delle tavole di mortalità… e non solo.
Un pensiero preliminare
Prima di affrontare l’argomento della Kaplan-Meier voglio fare una premessa. Lavorando spesso con questo strumento, sento il peso dei suoi protagonisti. Molte volte la curva Kaplan-Meier viene usata per tracciare la curva di sopravvivenza generale (tecnicamente indicata come overall survival) all’interno di studi clinici e l’outcome osservato è la morte del paziente. Perciò, quando tocca a me dare un parere statistico, molti pazienti coinvolti nel dataset non ci sono più. Questo articolo vuole essere una guida per chi si approccia a questo strumento, ma anche vuole essere un “grazie” a quei pazienti che con i loro dati contribuiscono al mondo della scienza.
Kaplan-Meier
La Kaplan-Meier è il metodo più famoso per analizzare dati “time-to-event“, ossia che considerano il tempo affinché un dato evento si verifichi. L’epidemiologia e la clinica ne fanno un grande uso, in quanto essa rientra all’interno dei metodi statistici per lo studio della sopravvivenza. Conoscere la curva di sopravvivenza Kaplan-Meier ed il modello di Cox significa disporre di buoni strumenti per trattare i dati “time-to-event”.
Informazioni Preliminari
Partiamo da una buona notizia: la curva Kaplan-Meier non teme i dati censored. La curva di sopravvivenza considera questa tipologia di dati fintanto che essi fanno parte del dataset, ossia fino all’ultima osservazione disponibile. Da quel momento in poi, i segmenti incompleti vengono ignorati, salvo collaborare nell’abbassare il numero dei soggetti a rischio allo tempo successivamente monitorato.
Il concetto alla base della Kaplan-Meier è la probabilità condizionata (vedi il riquadro sotto per la modalità di calcolo), cioè la probabilità di sopravvivere fino ad uno specifico momento condizionata alla probabilità di essere vivo nei precedenti periodi temporali.
Probabilità Condizionata: come si determina
Supponiamo di lanciare un dado per tre volte consecutive. La probabilità di avere “testa” è dello 0.50 (ossia 50%) nel primo lancio, dello 0.50 nel secondo e di 0.50 nel terzo. La probabilità cumulata di avere “testa” in tutti e tre i lanci è data dal prodotto delle probabilità, ossia:
0.50 ∙ 0.50 ∙ 0.50 = 0.125
Dunque la probabilità che lanciando un lancio tre volte esca “testa” è del 12.5%.
Assunzioni Necessarie
Come tutti gli strumenti statistici che si rispettano, anche questa curva di sopravvivenza ha le sue necessarie assunzioni affinché possa correttamente spiegare i dati.
La prima assunzione prevede che quando si usa il metodo Kaplan-Meier, i pazienti censored abbiano, in ogni intervallo temporale, la stessa prospettiva di sopravvivenza dei pazienti che continuano ad essere eseguiti nello studio. Non è un’assunzione semplice da controllare. Sul punto ti consiglio di valutare le motivazioni di fuoriuscita dei pazienti dello studio e di effettuare delle osservazioni di tipo clinico. Tralasciare una disamina di questo aspetto significa che eventuali bias possono condurre ad una sottostima della sopravvivenza.
La seconda assunzione prevede che la probabilità di sopravvivenza deve essere uguale per tutti i pazienti senza alcuna distinzione rispetto al loro momento di ingresso nello studio (prima fase o ultima fase). Questa assunzione deve essere necessariamente provata in fase di analisi.
Infine la terza assunzione comporta che l’evento osservato in uno specifico momento temporale sia accaduto esattamente in quel momento. Questo è semplice in alcuni casi (e.g. determinazione della morte), ma complesso in molti altri (si pensi a tutti quei casi in cui una recidiva è scoperta solo al momento del follow-up programmato). Ciò può portare ad una sovrastima della sopravvivenza.
La curva Kaplan-Meier
La curva Kaplan-Meier è una curva a gradini, una sorta di scala in cui ogni step rappresenta il verificarsi dell’outcome. Dunque, il numero di step rappresenta il numero di eventi di interesse che si sono verificati durante il follow-up. Sull’asse delle x viene indicato il tempo e sull’asse delle y è riportata la probabilità di sopravvivenza (probabilità condizionata).
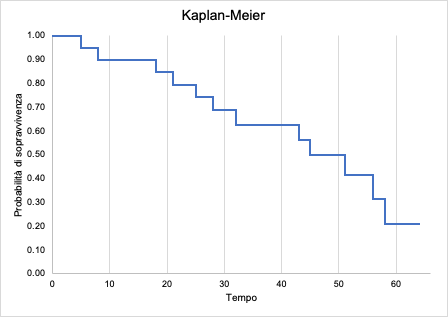
La lettura del plot è immediata: individuato un tempo, si va ad identificare la corrispondente probabilità di sopravvivenza. Tale lettura può essere anche invertita per la determinazione la sopravvivenza media: considera la probabilità al 50% ed identifica il tempo corrispondente. Quello ti darà la mediana del tempo osservato (ovviamente questa modalità di calcolo vale solo ed esclusivamente in questo caso, per il calcolo della mediana, vedi articolo).
Anche nel tracciare il plot vi sono delle accortezze da rispettare. Il plot deve essere esteso fino a quando vi è un ragionevole numero di pazienti che raggiunge l’ultimo follow-up riportato (proporzione del 10-20%). Nel caso di comparazioni tra diverse curve di sopravvivenza (e.g. pazienti con diverse caratteristiche), è necessario riportare le misure di incertezza, dunque errore standard o intervallo di confidenza al 95%.
Test di significatività: il Log-Rank
È possibile anche nel caso della Kaplan-Meier eseguire una comparazione tra due gruppi accompagnata da un test di significatività (famoso p-value). I due gruppi possono essere definiti genericamente come pazienti esposti e non-esposti con riferimento alla presenza o meno di una specifica problematica, e.g. si pensi alla severità della malattia o alla presenza di una data comorbidità.
Per determinare la significatività si ricorrere al log-rank test: l’ipotesi nulla prevede che la proporzione di individui per i quali l’evento si verifica dipende solo dalla dimensione dei gruppi (esposti vs non-esposti) e si assume che essa sia la stessa dell’intero campione (esposti + non-esposti). Un p-value minore di 0.05 comporta il rifiuto della precedente ipotesi nulla e dunque una differenza tra gruppi.
Conclusione
La curva Kaplan-Meier rappresenta un’importante tecnica statistica per la determinazione della sopravvivenza. Consente infatti di eseguire delle ipotesi eziologiche e prognostiche in campo della ricerca clinica ed epidemiologica, fornendo risposte accurate e precise sugli andamenti nel tempo e sulla probabilità di verifica di un determinato evento.






